1- آنچه در این آموزش خواهیم خواند…
فصل تحلیل سازههای کتاب استاتیک مریام در دو بخش آموزش داده شده است. بخش اول آموزش با عنوان تحلیل خرپا در استاتیک مریام به روش مفصل به همراه مثال، میباشد.
در این آموزش به بررسی و تحلیل خرپاهای دو بعدی به روش مفصل میپردازیم. در آموزش تحلیل سازهها (تحلیل خرپا) بخش دوم نیز به بررسی و تحلیل خرپاهای دو بعدی به روش مقطع خواهیم پرداخت.
2- تحلیل خرپاهای دو بعدی
هدف از تحلیل سازهها تعیین نیروهای داخلی (نیروهای عمل و عکسالعمل بین عضوهای یک سازه) است. لازم به ذکر است که ما در این آموزش تنها به تحلیل سازهای معین استاتیکی میپردازیم، و از بین انواع سازه تنها خرپاها را بررسی میکنیم.
خرپا (Truss) شبکهای است متشکل از اعضای میلهای مستقیم و دو نیرویی که انتهای آنها به هم مفصل شدهاست و مجموعا یک سازه صلب (پایدار) ایجاد میکنند.
انواع کاربرد خرپاها را میتوان در پلهای خرپایی، تاورکرین، دکل برق فشار قوی، بادبند ساختمانها، سازه نگهبان جهت پایدارسازی گود، سقف سالنها و… مشاهده نمود.

اعضا تشکیل دهنده یک خرپا میتواند انواع پروفیلهای ساختمانی مانند: پروفیلهای I شکل، قوطی، لوله، نبشی، پروفیلهای دوبل و… باشد. برای اتصال این اعضا به یکدیگر نیز میتوان از انواع روشهای اتصال مانند جوش، پیچ و پرچ استفاده نمود.
1-2- خرپاهای ساده
کوچکترین واحد ساختمانی خرپاهای دو بعدی، یک قاب صلب مثلثی است. صلب به این معنا که تحت اثر بارهای وارد به آن فرو نمیریزد و تغییر شکل عضوهای آن ناچیز است. بنابراین خرپایی که از یک مثلث پایه و دوتا دوتا اعضا که از یک طرف به مفاصل موجود و از یک طرف به یک مفصل جدید متصل میشود خرپای ساده گویند.
اگر تعداد عضوهای یک خرپا بیش از حد مورد نیاز برای حفظ پایداری آن باشد، خرپا نامعین استاتیکی است. عضو یا تکیهگاههای اضافی که برای تعادل خرپا ضروری نیستند (بتوان آن را حذف کرد بدون آنکه پایداری خرپا بهم بخورد) را عضو یا تکیهگاه زائد گویند.
در مسائل مربوط به خرپاها فرضیات زیر در نظر گرفته میشوند:
1) اعضا خرپا دو نیرویی هستند و دو نیرو باید هم راستای میله، هم اندازه و در جهت مخالف یکدیگر باشند.
2) هر عضو خرپا ممکن است تحت کشش یا فشار باشد. نیروی کششی را با T و نیروی فشاری را با C نمایش میدهیم. همچنین نیروی کششی یا فشاری داخلی هر عضو (مقطع در طول عضو) باید یکسان باشد .

3) از وزن اعضا صرف نظر میشود. اگر نتوان از وزن اعضا صرف نظر کرد در صورتی که جرم عضو یکنواخت باشد، وزن آن (W) را با دو نیرو هر یک به اندازه W/2 که به دو سر عضو وارد میشود جایگزین میکنیم.

در خرپاهای ساده خطوط محوری اعضا در محل اتصال باید همرس (متقارب) باشند. در این صورت اتصال به صورت یک مفصل فرض میشود.
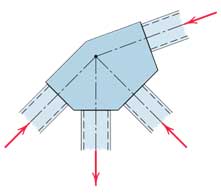
در تحلیل خرپای ساده فرض میشود که تمامی نیروهای خارجی به مفصلها وارد میشود. همچنین در خرپاهای بزرگ به دلیل تغییر شکلهای دمایی و تغییر شکلهای ناشی از بارهای وارده از یک تکیهگاه غلتکی استفاده میشود که در صورت نبودن آن سازه نامعین استاتیکی میباشد. (خرپا ساده پایدار و معین است اگر سه قید تکیهگاهی داشته باشد. به شرط بررسی آرایش قیدها )
3- تحلیل خرپاها به روش مفصل
این روش به تعادل نیروهای همرس در صفحه خرپا میپردازد و تنها دو معادله تعادل مستقل دارد. برای هر گره (مفصل) معادلات تعادل به شکل زیر خواهد بود:
در این روش از مفصلی شروع میکنیم که حداقل یکی از نیروهای وارده معلوم باشد و تعداد نیروهای مجهول آن از دو تا تجاوز نکند (مفصلی که حداکثر دو عضو مجهول به آن وصل باشد.). بنابراین گره آخر به کنترل درستی جوابها کمک میکند.
جهت نیرو با یک پیکان مشخص میشود. اگر نیرو کششی باشد، پیکان رسم شده از مفصل خارج میشود و اگر نیرو فشاری باشد، پیکان رسم شده به مفصل وارد میشود.
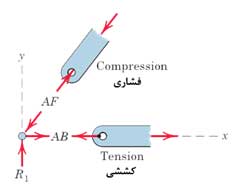
اگر جهت یک نیرو مشخص نبود یک جهت را فرض میکنیم اگر حاصل مقدار نیرو مثبت بود جهت فرضی درست بوده اگر حاصل منفی بود جهت فرضی غلط بوده و جهت صحیح عکس آن میباشد.
1-3- نامعینی داخلی و نامعینی خارجی در خرپاها
اگر تعداد تکیهگاههای خرپا بیشتر از تعداد لازم برای برقراری تعادل پایدار آن باشد، خرپا نامعین استاتیکی است و تکیه گاه اضافی موجب نامعینی خارجی خرپا میشود. اگر تعداد اعضا خرپا بیشتر از تعداد لازم برای پایداری آن باشد. خرپا نامعین استاتیکی است و عضو زائد موجب نامعینی داخلی خرپا میشود.
حال اگر تعداد قیدها را با r و تعداد اعضا را با m و تعداد گرهها را با j نمایش دهیم، تعداد مجهولات برابر m+r و تعداد معادلات مستقل تعادل برابر 2j خواهد بود. در این صورت سه حالت زیر را خواهیم داشت:
1) اگر شرط زیر برقرار باشد خرپا ناپایدار است
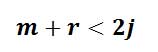
2) اگر شرط زیر برقرار باشد خرپا نامعین استاتیکی است. اما پایداری آن باید بررسی شود.
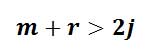
3) اگر شرط زیر برقرار باشد خرپا معین استاتیکی است. اما پایداری آن باید بررسی شود.
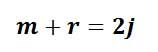
این معادله شرط لازم برای پایداری خرپا است اما شرط کافی نیست. زیرا ممکن است تعدادی از اعضا به گونهای در چیدمان خرپا باشند که بر پایداری آن تاثیر نداشته باشند.
2-3- شرایط ویژه در تحلیل خرپاها
در تحلیل خرپاها سه حالت ویژه وجود دارد که در زیر هر یک را بررسی میکنیم.
1) اگر دو عضو خرپا در یک امتداد باشند و خرپا یک عضو مایل بدون نیروی خارجی داشته باشد، معادلات تعادل به شکل زیر خواهند بود.
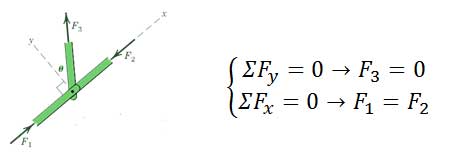
2) اگر خرپا مفصلی با دو عضو غیر هم راستا و بدون نیروی خارجی داشته باشد، معادلات تعادل به شکل زیر خواهند بود.
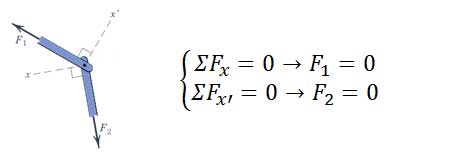
3) اگر خرپا مفصلی با چهار عضو دو به دو هم راستا و بدون نیروی خارجی داشته باشد، معادلات تعادل به شکل زیر خواهند بود.
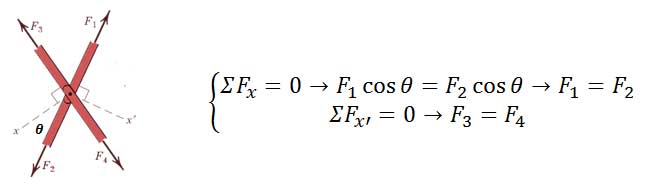
اعضای ضربدری که برای مقابله با نیروی جانبی در سازه (از جمله خرپا) استفاده میشود را بادبند گوییم. اگر اعضا بادبند بتواند همزمان فشار و کشش را تحمل کند سازه نامعین استاتیکی است. اما اگر اعضا بادبند انعطاف پذیر باشد (مانند کابل) عضوی که تحت فشار است حذف شده و عضو تحت کشش بررسی میشود.
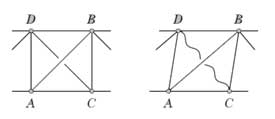
برای حل اینگونه مسائل به دو روش میتوان عمل کرد:
روش اول این است که با تشخیص عضو فشاری با توجه به نیروهای وارده و هندسه خرپا آن را حذف کنیم و مسئله را حل نماییم.
روش دوم این است که به دلخواه یکی از اعضا بادبند را حذف کرده برای دیگری نیروهای داخلی را محاسبه میکنیم. اگر حاصل منفی شد اشتباه انتخاب کردهایم اگر مثبت بود انتخاب درست بوده است.
4- مسائل
برای فهم بهتر حل مسائل میتوانید به ویدیو مراجعه کنید.
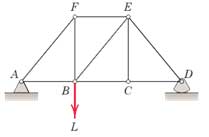
1-4- مسئله 1
در خرپای زیر نیروهای داخلی هر یک از عضوها را به روش مفصل تعیین کنید.
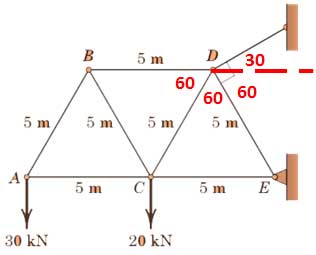
ابتدا عکس العملهای تکیهگاهی را محاسبه میکنیم.
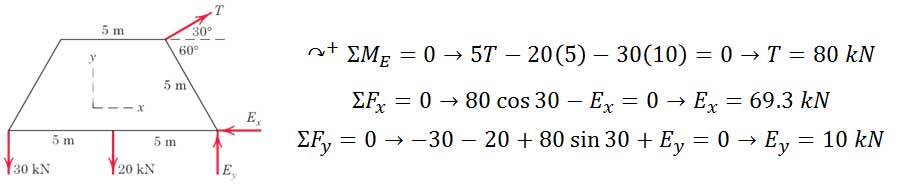
در گره (مفصل) A
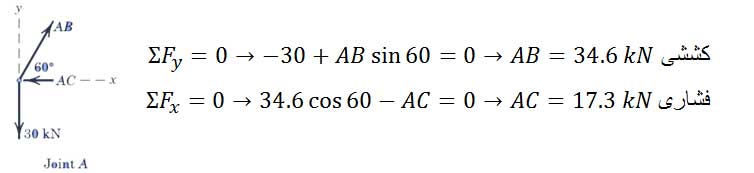
در گره (مفصل) B

در گره (مفصل) C
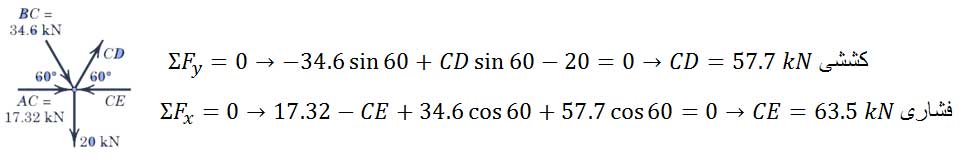
در گره (مفصل) E
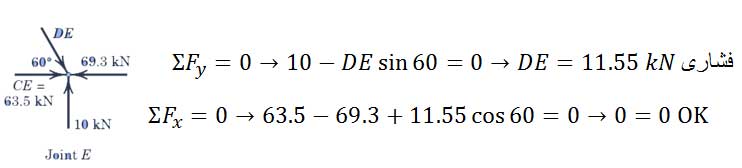
2-4- مسئله 2
با روش مفصل نیروی داخلی در عضو CG از خرپای زیر را تعیین کنید. فرض کنید که اندازه چهار عکس العمل خارجی در تکیهگاههای A ،B ،E و F یکسان است و راستای این عکس العمل ها بر سطح تکیهگاهی آن ها عمود است.
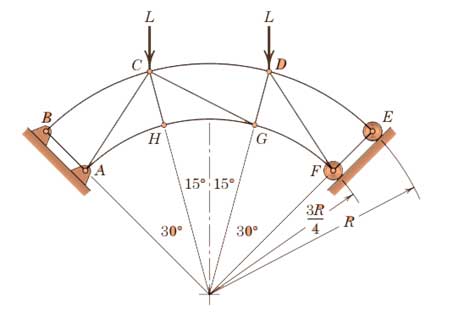
برای مشاهده حل این سوال به صفحه آموزش (حل تمرین استاتیک تمامی فصلها) مراجعه کنید.