مقاومت مصالح بیر جانسون فصل 3 پیچش: زاویه پیچش در محدوده‌ی الاستیک – پیچش در محورهای نامعین استاتیکی

1- آنچه در این آموزش خواهیم خواند…

این آموزش بخش دوم از فصل سوم کتاب مقاومت مصالح بیر جانسون با عنوان پیچش (زاویه پیچش در محدوده الاستیک – پیچش در محور نامعین استاتیکی) می‌باشد. در این آموزش درباره زاویه پیچش در محدوده‌ی الاستیک و پیچش در محورهای نامعین استاتیکی بحث خواهیم داشت. در بخش گذشته به بررسی بحث مقدماتی تنش در محورهای گرد، تغییر شکل در محور گرد و تنش‌های محدوده‌ی الاستیک پرداختیم.

2- زاویه پیچش در محدوده‌ی الاستیک

میخواهیم رابطه بین زاویه پیچش φ محور گرد و گشتاور پیچشی T را تعیین کنیم. همانند قسمت قبل فرض می‌کنیم که محور گرد به صورت الاستیک باقی بماند (محوری با طول L و شعاع c تحت پیچش T).

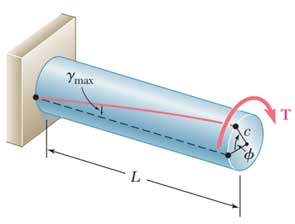
از قبل رابطه بین کرنش برشی حداکثر و زاویه پیچش را داریم:

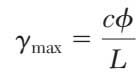
همچنین از قبل با توجه به قانون هوک داریم:

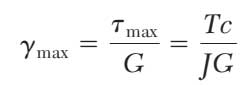
با تساوی قرار دادن سمت راست دو معادله رابطه مورد نظر تعیین می‌شود که در آن زاویه پیچش بر حسب رادیان است.

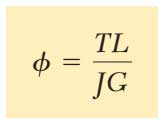
از این روش برای تعیین ضریب صلبیت G یک ماده استفاده می‌شود.

از این رابطه تنها زمانی می‌توان استفاده کرد که محور همگن بوده مقطع یکنواختی داشته و تنها از یک انتها بارگذاری شده باشد. اگر گشتاورهای پیچشی در محل‌های دیگری به جز دو انتهای محور وارد شوند و یا محور از چند بخش با مقاطع و یا مواد مختلف تشکیل شده باشد، باید آن را به بخش‌های جداگانه تقسیم کرد که هر بخش شرایط لازم برای استفاده از رابطه برخوردار باشد. در همچین شرایطی زاویه پیچش به کمک رابطه زیر قابل محاسبه است.

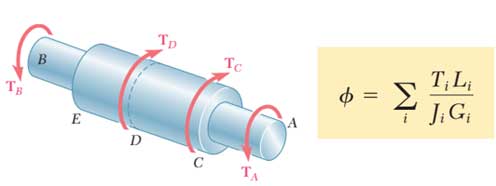
برای محور با سطح مقطع متغیر داریم:

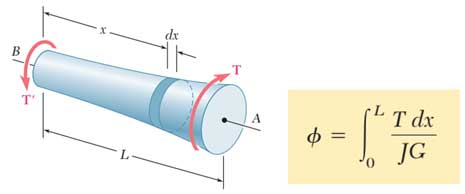
در رابطه حاصل شده محور مورد نظر از یک انتها به تکیه گاه ثابتی متصل بود بنابراین در هر حالت زاویه‌ی پیچش با زاویه‌ی چرخش انتهای آزاد آن برابر بود. حال اگر هر دو انتهای محور بچرخند زاویه‌ی چرخش محور برابر است با زاویه‌ی چرخش یک انتهای آن نسبت به انتهای دیگر.

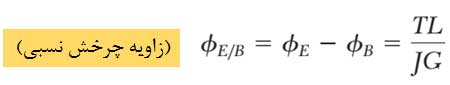
3- پیچش در محورهای نامعین استاتیکی

اگر محور نامعین استاتیکی باشد یعنی گشتاورهای پیچشی خارجی (گشتاورهای پیچشی وارد بر محور از طرف تکیه‌گاه) را نتوان با کمک نمودار جسم آزاد تعیین کرد، باید از معادلات تعادل همراه با روابط تغییر شکل محور (با توجه به هندسه) استفاده نمود.

4- مسئله 3-5

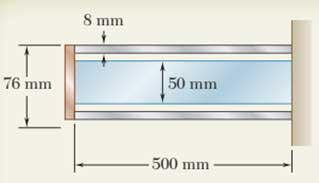
محوری فولادی و لوله‌ای آلومینیمی به صورت نشان داده شده در تصویر مقطع برش خورده به تکیه‌گاه ثابت و دیسکی صلب متصل‌اند. با فرض صفر بودن تنش‌های اولیه و تنش برشی مجاز 120MPa محور فولادی و 70MPa لوله‌ی آلومینیمی، حداکثر مقدار گشتاور پیچشی T₀ قابل اعمال به دیسک را تعیین کنید. برای فولاد از G=77GPa و برای آلومینیم از G=27GPa استفاده کنید.

نمودار جسم آزاد دیسک را رسم می‌کنیم:

براساس تغییر شکل‌ها داریم: (لوله و محور هر دو به دیسک صلب متصل هستند.)

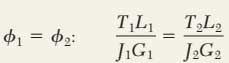
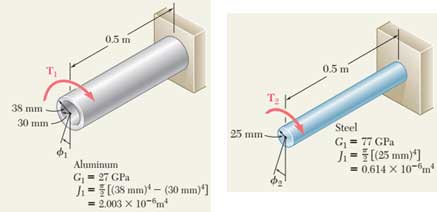
با محاسبه ممان اینرسی قطبی برای محور و لوله داریم:

بنابراین:

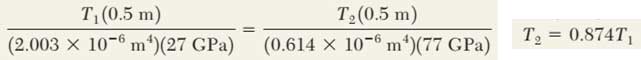
براساس تنش برشی: با فرض اینکه در آلومینیم τ≤70MPa حالت بحرانی داشته باشد:

مشخص است که از تنش برشی مجاز فولاد یعنی 120MPa تجاوز شده است و فرض ما اشتباه بوده است. بنابراین حداکثر گشتاور پیچشی T₀ را با استفاده از τ_steel=120MPa  به دست می‌آوریم

5- مراجع

Beer, Ferdinand, P. and Johnston, E, Russell. and DeWolf, John. and Mazurek, David. (2020). Mechanics of Materials. 8th Edition. McGraw Hill