1- آنچه در این آموزش خواهیم خواند…
فصل سوم کتاب استاتیک مریام در دو بخش آموزش داده شده است. این آموزش با عنوان تعادل در استاتیک مریام بخش 2 | شرایط تعادل استاتیکی، بخش دوم میباشد.
در آموزش تعادل بخش اول شیوه رسم دیاگرام جسم آزاد را شرح دادیم و در ادامه بحث نیز شرایط تعادل جسم را بررسی کردیم. اکنون در این آموزش به شرح مباحث قیدهای تکیهگاهی، معین و نامعین استاتیکی که بخشهای بعدی شرایط تعادل هستند، خواهیم پرداخت. در نهایت نیز نمونه مسائل حل خواهند شد.
3- شرایط تعادل
4-3- مشخصات قیدهای تکیهگاهی
همانطور که قبلا گفتیم معادلات تعادل شرایط لازم وکافی برای برقراری تعادل یک جسم هستند. اما این معادلات تمامی اطلاعات مورد نیاز برای محاسبه نیروهای نامعلوم را نمیدهد. حال سوال اینجاست که آیا معادلات تعادل برای تعیین همه مجهولات کافی است؟
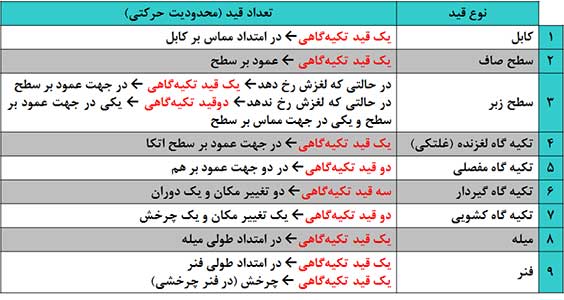
پاسخ این است که بستگی به مشخصات قیدهای حرکتی دارد. قیدهای حرکتی (قیدهای تکیهگاهی) محدودیتی است که از طرف تکیهگاهها برای حرکت جسم بوجود میآید. در یک مسئله تعداد مجهولات برابر تعداد قیدها است. لازم به ذکر است که تعداد قیدها عکس تعداد درجات آزادی است. اما باید در شمارش تعداد قیود به قیدهای زائد نیز توجه داشت. قیدی را که بتوانیم آن را حذف کنیم بدون اینکه تعادل سیستم بهم بخورد، قید زائد گوییم.
بنابراین: تعداد قید زائد = تعداد مجهولات – تعداد معادلات مستقل تعادل
در جدول زیر انواع قیدهای تکیهگاهی آورده شده است.
5-3- سازههای معین و نامعین استاتیکی
جسمی را معین استاتیکی گوییم که تعداد قیدهای تکیه گاهی (مجهولات) با تعداد معادلات مستقل تعادل برابر باشد. همچنین جسمی را نامعین استاتیکی گوییم که تعداد قیدهای تکیه گاهی (مجهولات) بیشتر از تعداد معادلات مستقل تعادل باشد (قید زائد داریم). بنابراین درجه نامعینی جسم برابر است با تعداد قیدهای زائد.
اما حال باید به این نکته توجه کنیم که شرط لازم برای تعادل این است که حداقل به تعداد معادلات مستقل تعادل قید تکیه گاهی (مجهول) داشته باشیم. یعنی: تعداد مجهولات ≥ تعداد معادلات مستقل تعادل
این شرط برای تعادل لازم است اما کافی نیست. زمانی قیدها برای تعادل جسم کافی هستند که چیدمان (آرایش) قیدها نیز مناسب باشد. به این نکته نیز توجه کنید که برای سازهای که شرط لازم تعادل را ندارد بحث معین و نامعین بود وارد نمیشود.
6-3- شیوه حل مسائل
اگر جسم ما معین استاتیکی باشد، با استفاده از معادلات تعادل به حل سوال میپردازیم. حال اگر جسم نامعین استاتیکی بود، علاوه بر معادلات مستقل تعادل نیاز به معادلات سازگاری و روابط مشخصه (نیرو-جابجایی) داریم که مبحث درس مقاومت مصالح است.
بنابراین برای حل سوال به ترتیب زیر عمل میکنیم:
1- ابتدا دیاگرام جسم آزاد را رسم میکنیم.
2- معادلات مستقل تعادل را تعیین میکنیم
3- چک میکنیم که سازه شرط لازم برای تعادل را دارد یا خیر؟
4- بررسی میکنیم که آیا سازه معین استاتیکی یا خیر؟
5- و در نهایت با توجه به شرایط موجود مسئله را حل مینماییم.
7-3- شرایط خاص در تعیین تعادل سازه
در تعادل سازه دو حالت خاص ممکن است وجود داشته باشد:
حالت اول: عکس العمل های متقارب (همرس)
در صورتی که کلیه قیدها (نیروهای عکس العمل) متقارب باشند سازه (جسم صلب) تنها درصورتی تعادل دارد که نیروهای معلوم وارده نیز در همان نقطه متقارب شوند. بنابراین اگر نیروها وارده با عکس العمل ها متقارب بودند، شرط تعادل را کنترل میکنیم. اما اگر نیروها وارده با عکس العمل ها متقارب نبودند، شرط تعادل تامین نمیشود زیرا برآیند لنگرها به هیچ عنوان صفر نمیشود. (نیروهای معلوم حوله نقطه تقارب لنگر ایجاد میکنند)
حالت دوم: عکس العمل های موازی
در صورتی که کلیه قیدها (نیروهای عکس العمل) موازی باشند سازه (جسم صلب) تنها درصورتی تعادل دارد که نیروهای معلوم وارده نیز موازی قیدها باشند. بنابراین اگر نیروها وارده با عکس العمل ها موازی بودند، شرط تعادل را کنترل میکنیم. اما اگر نیروها وارده با عکس العمل ها موازی نبودند، شرط تعادل تامین نمیشود زیرا برآیند نیروها در امتداد عمود بر نیروهای عکس العمل به هیچ عنوان صفر نمیشود.
4- مسائل شرایط تعادل
برای فهم بهتر حل مسائل میتوانید به ویدیو مراجعه کنید.
1-4- مسئله 1
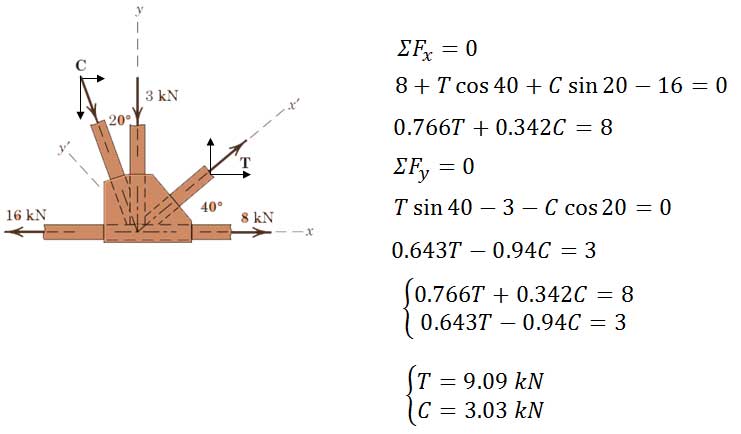
اگر نیروهای وارد به مفصل خرپایی که در حال تعادل است به گونه ای باشد که در شکل میبینید. اندازه نیروهای C و T را تعیین کنید.
روش اول: روش اسکالر
روش دوم: روش اسکالر
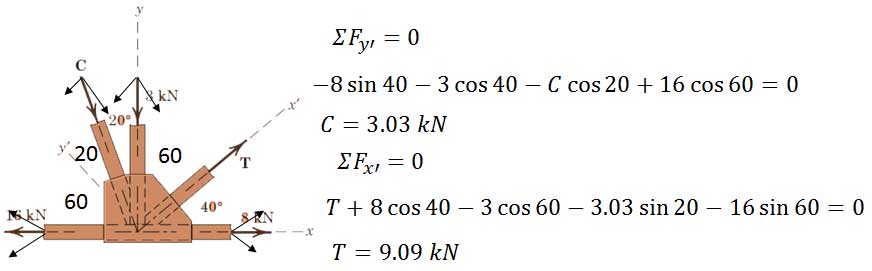
روش سوم: روش برداری
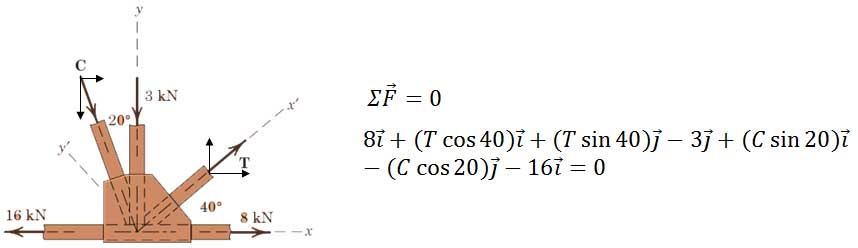
ضرایب بردارهای واحد i و j را برابر صفر قرار میدهیم

روش چهارم: روش هندسی
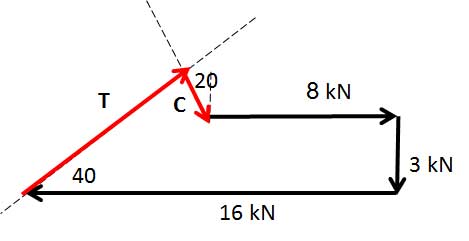
با استفاده از چند ضلعی نیروها به روش زیر عمل میکنیم:
ابتدا بردارهای معلوم با یک مقیاس مناسب از سر یکی به ته دیگری رسم میکنیم.
راستای نیروهای C و T را به گونه ای رسم میکنیم که چند ضلعی بسته شود.
با اندازه گیری طول این بردارها از محل برخورد مقادیر مجهول C و T حاصل میشود.
2-4- مسئله 2
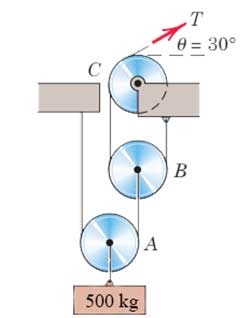
مجموعهای از قرقرهای متصل به هم در شکل نشان داده شده است. چنانچه هر یک از قرقرها بتواند آزادانه حول محور خود بچرخد و از وزن آنها صرف نظر شود، کشش T را تعیین کنید و اندازه نیروی وارد به محور قرقره C را بدست آورید.
نمودار جسم آزاد هریک از قرقرها را رسم میکنیم.
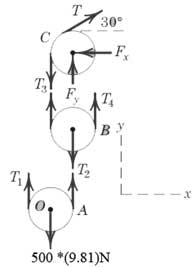
از قرقره A شروع میکنیم. (شعاع r) (جهت ساعتگرد را مثبت فرض میکنیم)
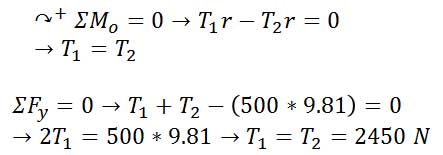
قرقره B
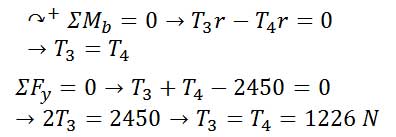
قرقره C
زاویه θ بر گشتاور T حول مرکز قرقره تاثیرگذار نیست.
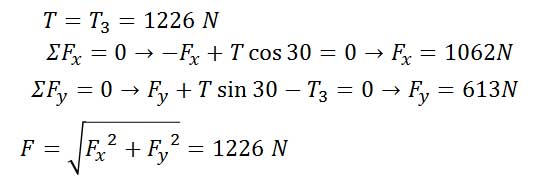
3-4- مسئله 3
هنگامی که قاب AOC با جرم 0.5kg در تماس با تکیه گاه C است، فنر خطی به انداره 10 میلیمتر کشیده شده است. نیروی موردنیاز P برای جداکردن قاب از تکیه گاه C را در دوحالت الف) با در نظر گرفتن وزن قاب ب) با چشم پوشی از آن تعیین کنید.
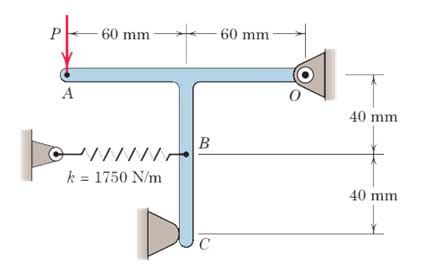
برای مشاهده حل این سوال به صفحه آموزش (حل تمرین استاتیک تمامی فصلها) مراجعه کنید.
ادامه مباحث این فصل در سه بعد مطرح میشود که فعلا آنها را بیان نمیکنیم. اگر نیاز به آموزش این مباحث دارید در بخش نظرات به ما اطلاع دهید تا در زمان مناسب مبحث آموزشی آن را برای شما آماده کنیم.