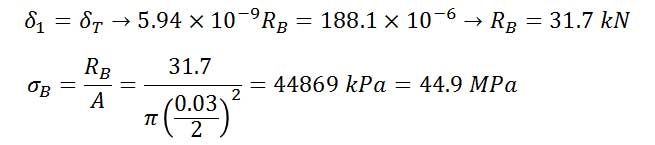1- آنچه در این آموزش خواهیم خواند…
فصل دوم کتاب مقاومت مصالح بیر جانسون با عنوان تنش و کرنش – بارگذاری محوری در 7 آموزش بررسی شده است. این آموزش بخش چهارم از این فصل میباشد. در این آموزش درباره مسائل نامعین استاتیکی و مسائل شامل تغییر دما در مقاومت مصالح توضیح داده شده است. بخش سوم از فصل دوم مقاومت مصالح بارگذاری تکراری، خستگی / تغییر شکل اعضا در بارگذاری محوری میباشد.
2- مسائل نامعین استاتیکی
مسائل نامعین استاتیکی تنها با معادلات تعادل قابل حل نیستند. در مسائل نامعین استاتیکی تعداد مجهولات (قیدها) بیشتر از معادلات مستقل تعادل میباشد. برای حل مسائل نامعین استاتیکی باید از معادلات تعادل به همراه معادلات سازگاری تغییر شکلها که رابطه بین تغییر شکلهای سازه و هندسه آن است، استفاده نمود. در تحلیل سازهای نامعین استاتیکی ابعاد مقطع و خصوصیات مصالح اثر گذارند.
برای حل مسائل نامعین استاتیکی از روش برهمنهی یا اصل جمع آثار (super position) نیز استفاده میشود. در سازه نامعین، تعداد تکیهگاهها بیشتر از تعداد مورد نیاز برای تعادل سازه است. در این حالت تعداد قیود اضافی حذف شده و این واکنش اضافی به صورت بار مجهول در نظر گرفته میشود. برای تحلیل اثر جداگانه تغییر شکلهای ناشی از بارهای مفروض و واکنشهای اضافی محاسبه شده و با هم جمع میشوند. استفاده از این روش شرایطی دارد که در بخش قانون عمومی هوک صحبت خواهد شد.
3- مسئله 2
برای فهم بهتر پاسخ سوالات به ویدیو آموزش مراجه کنید.
تغییر شکل میله و لوله در اثر اعمال نیروی P به صفحه صلب انتهایی چقدر است؟

نمودار جسم آزاد هر سه عضو را رسم میکنیم. داریم:
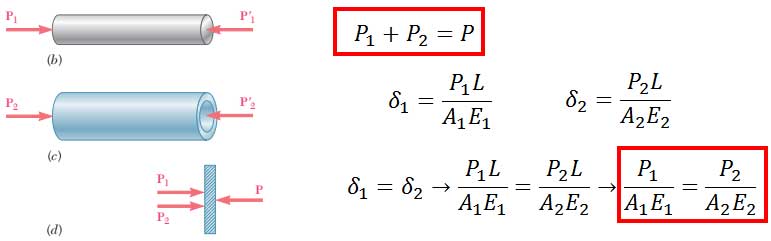
از حل همزمان معادلاتی که در کادر قرمز رنگ هستند داریم:
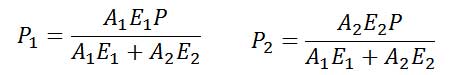
حال برای تعیین تغییر شکل یکسان لوله و میله میتوان مقادیر محاسبه شده را در معادلات δ1 یا δ2 قرار داد.
4- مسائل شامل تغییر دما
میله AB همگن با مقطع یکنواخت میباشد و آزادانه روی سطح افقی قرار دارد. با افزایش دما به اندازه ΔT طول میله به اندازه δT افزایش مییابد.
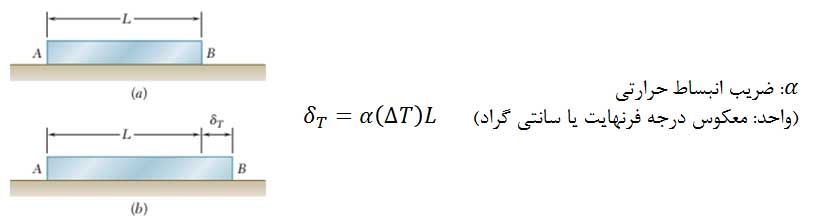
در این صورت کرنش حرارتی به صورت زیر خواهد بود:
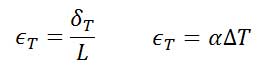
در این حالت کرنش ایجاد شده با هیچ تنشی همراه نیست.
حال حالت زیر را در نظر میگیریم. میله AB همگن با مقطع یکنواخت میباشد که بین دو تکیهگاه ثابت قرار دارد. با افزایش دما به اندازه ΔT باتوجه به مقید بودن میله δT=0 خواهد بود.
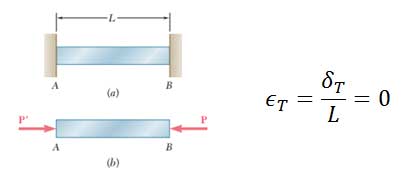
در این حالت تنش بدون کرنش میباشد.
برای محاسبه تنش ناشی از تغییر دما در این حالت با توجه به اینکه میله در بین دو تکیهگاه صلب میباشد، مسئله از نظر استاتیکی نامعین است. بنابراین از روش برهم نهی استفاده میکنیم. تکیهگاه B حذف شده و بجای آن یک نیروی معادل قرار میدهیم. داریم:
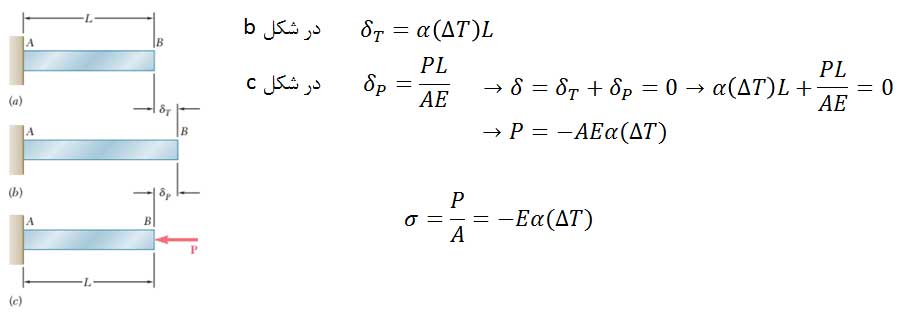
رابطه تنش محاسبه شده برای میله همگن با مقطع یکنواخت قابل استفاده است.
5- مسائله 3
برای فهم بهتر پاسخ سوالات به ویدیو آموزش مراجه کنید.
در حالتی که دمای میله فولادی 20 درجه سانتی گراد باشد، دمای استوانه برنجی تا 50 درجه سانتی گراد افزایش داده میشود. با فرض اینکه پیش از تغییر دما هیچ تنشی وجود نداشته باشد، مقدار تنش در استوانه برنجی چقدر است؟
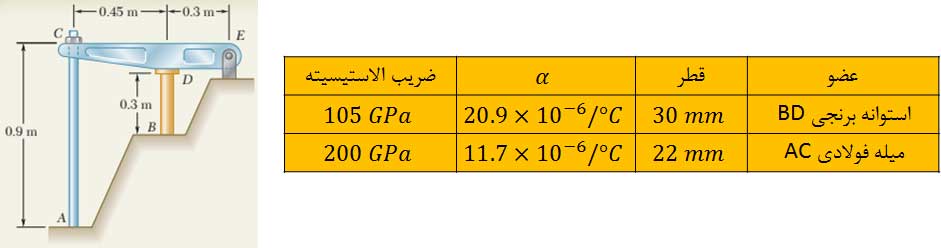
دیاگرام آزاد جسم رسم میشود.
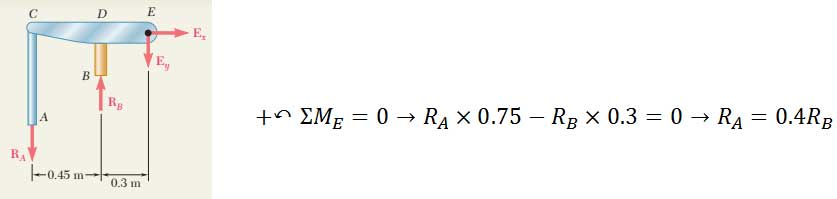
با توجه به اینکه مقدار تنش در استوانه برنجی خواسته شده باید:
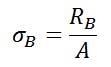
با استفاده از اصل جمع قوا اقدام به حل مسئله میکنیم. RB به عنوان واکنش اضافی حذف میکنیم. با افزایش دما، نقطه B به اندازه δT به سمت پایین حرکت میکند. با توجه به اینکه تغییر مکان نقطه B صفر است، δ1 ناشی از RB باید با δT برابر باشد.
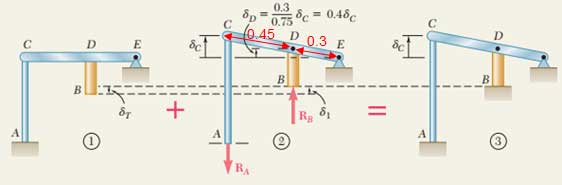

همچنین گفتیم که با توجه به اینکه تغییر مکان نقطه B صفر است، δ1 ناشی از RB باید با δT برابر باشد.