1- آنچه در این آموزش خواهیم خواند…
فصل پنجم از کتاب استاتیک مریام به بحث نیروهای گسترده پرداخته است. این فصل را در سه آموزش بررسی میکنیم. عنوان دومین آموزش، تحلیل تیر و اصول رسم نمودار برش و خمش در استاتیک مریام بخش 2 میباشد. در این آموزش مباحث نیروهای خارجی و داخلی وارد به تیرها بررسی خواهند شد. در آموزش نیروهای گسترده بخش اول مباحث مرکز جرم و مرکز هندسی را شرح دادیم. همچنین در آموزش نیروهای گسترده بخش سوم نیز به حل مسئله رسم نمودار نیروی برشی و لنگر خمشی میپردازیم.
2- نیروهای خارجی وارد به تیرها
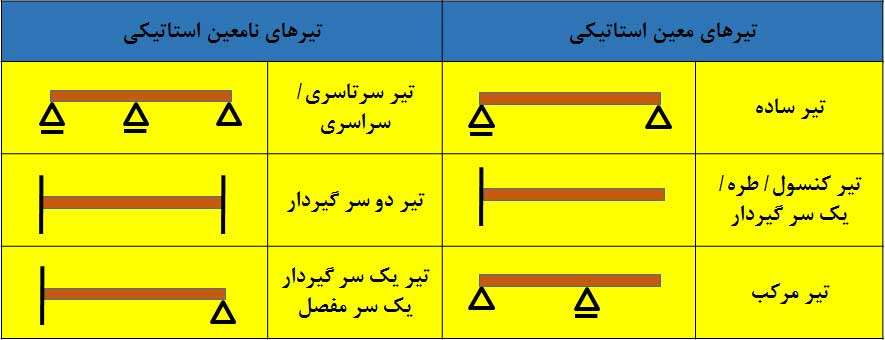
تیرها (Beams) عضوهایی از سازه هستند که در اثر نیروهای وارده تحت خمش قرار میگیرند. اگر قیدهای تکیهگاهی یک تیر را بتوان به کمک معادلات تعادل محاسبه کرد تیر معین استاتیکی است. همچنین اگر تعداد قیدهای تکیهگاهی بیشتر از تعداد مورد نیاز برای برقراری تعادل تیر باشد، تیر نامعین استاتیکی است. در جدول زیر نمونههایی از تیرهای معین و نامعین استاتیکی را مشاهده میکنید.
تیرها از نظر نوع بارگذاری خارجی دو دسته هستند. تیر با بارهای متمرکز و تیر با بارهای گسترده.
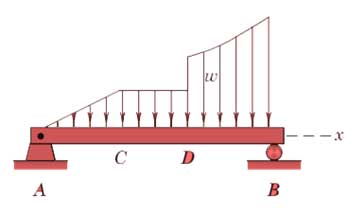
در شکل زیر شدت بار گسترده ω بر حسب نیرو بر واحد طول (طول/نیرو) بیان میشود. شدت بارگذاری در قسمت CD ثابت اما در AC و BD متغییر است. شدت بارگذاری در نقطه D ناپیوسته است. در نقطه C اگرچه شدت بار پیوسته است اما آهنگ تغییرات بار (dω/dx) ناپیوسته است.توزیع نیرو در قسمت CD توزیع ثابت، در قسمت AC توزیع خطی و در قسمت DB توزیع سهمی است.
در تحلیل بارگذاری گسترده به جای هر جزء بار گسترده، بار متمرکز معادل آن را قرار میدهیم. مقدار بار متمرکز معادل برابر با مساحت زیر نمودار شدت بار است. محل اثر بار متمرکز معادل در مرکز سطح ناحیه زیر نمودار شدت بار میباشد. سه نمونه از متداولترین بارهای گسترده به همراه برآیند آنها بررسی شده است.
در بارگذاری مستطیلی و مثلثی اندازه بار برآیند R به صورت مساحت حاصل از ضرب شدت بار ω (نیرو بر واحد طول تیر) در طولی از تیر L که بار بر روی آن توزیع شده است، بیان می شود. مشخص است که نیروی برآیند از مرکز هندسی این سطح میگذرد.
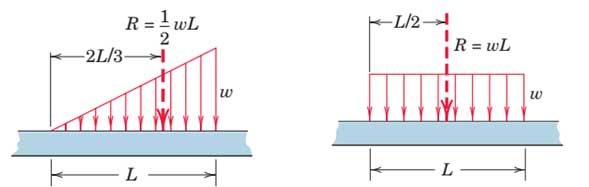
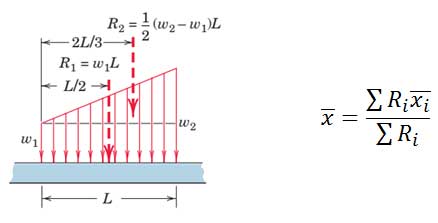
در بارگذاری ذوزنقهای مساحت ذوزنقه را به دو مساحت مثلثی و مستطیلی تقسیم میکنیم و نیروهای برآیند R1 و R2 مربوط به هر یک از این مساحتها را به طور جداگانه تعیین میکنیم. توجه داشته باشید که تک نیروی برآیند R با استفاده از روش تعیین مرکز هندسی سطوح مرکب با کمک رابطه زیر قابل محاسبه است. اما در بیشتر موارد نیازی به تعیین یک تک نیروی برآیند نیست.
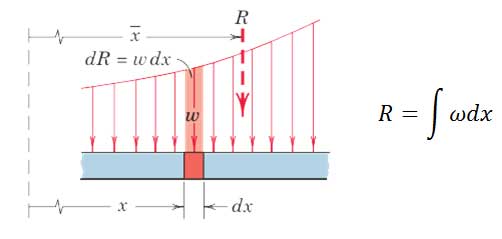
در شکل کلیتر از نحوه توزیع بار شکل زیر ابتدا یک دیفرانسیل نیرو به صورت dR=ωdx تعریف میکنیم سپس بار برآیند R را از مجموع این نیروهای دیفرانسیلهای نیرو بهدست می آوریم. یعنی:
همچنین با استفاده از اصل گشتاورها مرکز هندسی سطح بار حاصل میشود.
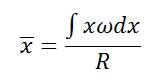
3- مسائل
برای فهم بهتر حل مسائل میتوانید به ویدیو مراجعه کنید.
1-3- مسئله 5
عکس العملهای تکیهگاهی تیر زیر را بدست آورید.
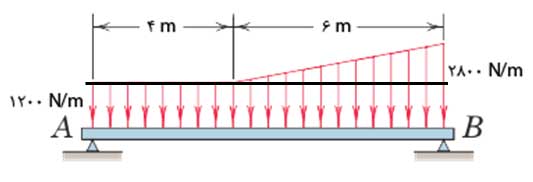
برای بار یکنواخت مستطیلی:
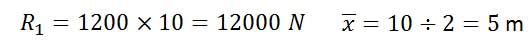
برای بار خطی مثلثی:
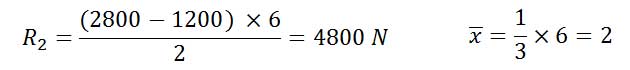
محاسبه عکس العملهای تکیهگاهی:

2-3- مسئله 6
به تیر زیر یک بار متمرکز، یک بار گسترده بیضوی و یک کوپل وارد میشود. نیروی P را چنان تعیین کنید که عکس العمل تکیهگاهی در B صفر شود.
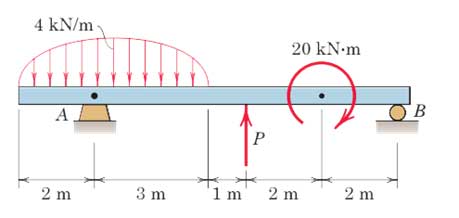
برای مشاهده حل این سوال به صفحه آموزش (حل تمرین استاتیک تمامی فصلها) مراجعه کنید.
4- نیروهای داخلی در تیرها
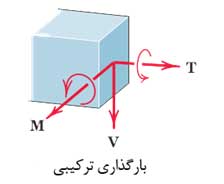
نیروهای داخلی در تیرها به چهار نوع تقسیم میشوند. نیروی محوری که بهصورت کششی یا فشاری است، نیروی برشی V، نیروی خمشی M و نیروی پیچشی T ازجمله نیروهای داخلی تیرهاست.

این نیروهای داخلی در شکل زیر نیز بهصورت مولفههای برداری برآیند نیروهای وارد بر مقطع عرضی تیر نمایش داده شدهاند.
5- نمودارهای نیروی برشی و گشتاور خمشی
نمودار تغییرات نیروی برشی و گشتاور خمشی برحسب متغییر فاصله از ابتدای تیر، به ترتیب نمودار نیروی برشی و گشتاور خمشی نمایده میشود.
برای رسم این دو نمودار ابتدا عکس العملهای تکیهگاهی از طریق نوشتن معادلات تعادل برای دیاگرام جسم آزاد کل تیر محاسبه میگردد. سپس در یک مقطع دلخواه تیر را برش زده و دیاگرام آزاد بخش سمت چپ یا راست این مقطع را رسم میکنیم. پس از آن معادلات تعادل نوشته میشود. این معادلات نیروی برشی و گشتاور خمشی را به ما میدهد.
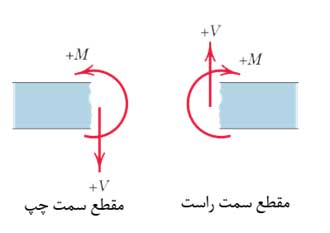
بهتر است قسمتی از تیر انتخاب شود که تعداد نیروی کمتری دارد. همچنین در محلی که نیرو یا گشتاور متمرکز وجود دارد نباید مقطع زد زیرا در این نقاط نمودار نیروی برشی و یا نمودار گشتاور خمشی دارای ناپیوستگی است. بنابراین مقطع باید در مرز این نقاط (قبل یا بعد از آن) زده شود. در این نقاط نمودارها جهش دارند. در محاسبات مربوط به تعیین نیروی برشی و لنگر خمشی از علامت قراردادی مثبت همانند شکل زیر استفاده میشود.
6- روابط بین نیروی برشی و گشتاور خمشی در تیرها تحت یک بارگذاری کلی
برای هر تیری که تحت بارهای گسترده باشد، میتوان روابطی نوشت که تعیین نیروی برشی و گشتاور خمشی در هر مقطع از طول تیر را امکانپذیر سازد. در شکل زیر نمودار آزاد بخش کوچکی از یک تیر به طول dx را نشان میدهد. با نوشتن معادله تعادل نیروها داریم:
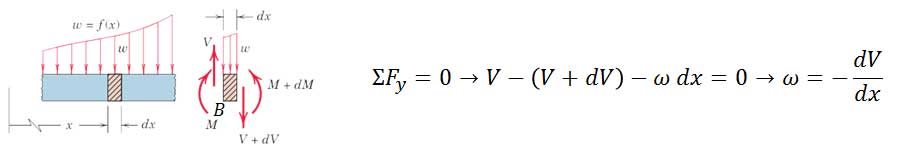
از معادله فوق در مییابیم که شیب نمودار نیروی برشی در هر نقطه با مقدار منفی بار وارده در آن نقطه برابر است. این معادله به جز در نقاط تحت بار متمرکز معتبر است زیرا در این نقاط به دلیل تغییر ناگهانی نیروی برشی، یک ناپیوستگی در نمودار بوجود میآید.
با انتگرالگیری از رابطه بالا خواهیم داشت:
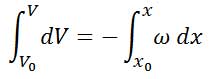
یا به عبارت دیگر
(مساحت زیر نمودار بار گسترده بین x و x0) – ( نیروی برشی در نقطه x0) = نیروی برشی در نقطه x
حال با معادله تعادل گشتاورها داریم:
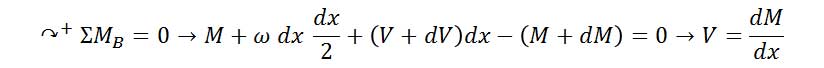
در معادله بالا از دیفرانسیلهای مرتبه دو صرف نظر میکنیم.
از معادله فوق در مییابیم که در هر نقطه از تیر نیروی برشی با شیب منحنی گشتاور خمشی برابر است. این معادله به جز در نقاط تحت کوپل متمرکز معتبر است زیرا در این نقاط به دلیل تغییر ناگهانی لنگر خمشی، یک ناپیوستگی در نمودار بوجود میآید.
با انتگرالگیری از رابطه بالا خواهیم داشت:
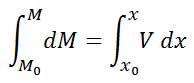
یا به عبارت دیگر
(مساحت زیر نمودار نیروی برشی بین x و x0) + ( لنگر خمشی در نقطه x0) = لنگرخمشی در نقطه x
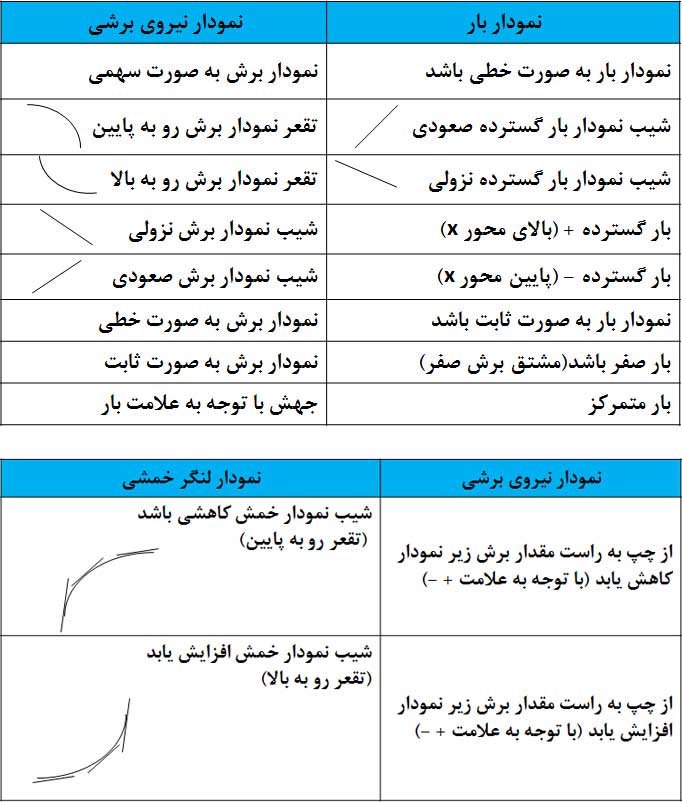
به یاد داشته باشید که با محاسبه مساحت زیر نمودار نیروی برشی میتوان نمودار لنگر خمشی را رسم نمود. همچنین مقادیر بحرانی در نمودار لنگر خمشی در محل تقاطع نمودار نیروی برشی با محور افقی دستگاه مختصات است. بر حسب x درجه نیروی برشی یکی بیشتر از بار وارده به تیر و درجه لنگر خمشی یکی بیشتر از نیروی برشی و دو درجه بیشتر از بار وارد به تیر است. بنابراین با دوبار انتگرال گیری از نمودار بار میتوان نمودار لنگر خمشی را محاسبه نمود. به عناون یک نکته خوب است بدانیم که آزمون مشتق اول نیز در تفسیر و رسم نمودارها کمک کننده است.
در دو جدول زیر نیز نکاتی کمک کننده برای رسم نمودار برش و خمش آورده شده است.