1- آنچه در این آموزش خواهیم خواند…
فصل پنجم از کتاب استاتیک مریام به بحث نیروهای گسترده پرداخته است. این فصل را در سه آموزش بررسی میکنیم. عنوان اولین آموزش، نیروهای گسترده، مرکز جرم و مرکز هندسی در استاتیک مریام بخش 1 میباشد. در این آموزش مباحث مرکز جرم و مرکز هندسی را شرح خواهیم داد. در آموزش نیروهای گسترده بخش دوم مباحث نیروهای خارجی و داخلی وارد به تیرها بررسی خواهند شد. در آموزش نیروهای گسترده بخش سوم نیز به حل مسئله رسم نمودار نیروی برشی و لنگر خمشی میپردازیم.
2- نیروهای گسترده
نیرویی که ابعاد محل اثر آن نسبت به ابعاد جسم ناچیز است را نیروی متمرکز یا نقطهای (Concentrated Force) گوییم. همچنین باید توجه نمود که به صورت واقعی نیروی متمرکز نداریم. در هنگامی که نیروها بر ناحیهای از جسم که در مقایسه با سایر ابعاد آن قابل ملاحظه است وارد شوند را باید به صورت گسترده درنظر گرفت. نیروهای گسترده شامل نیروهای خطی، نیروهای سطحی و نیروهای حجمی (Body Force) است. باید بدانیم که توزیع نیرو به معنای تقسیم و گسترش نیرو در یک سطح، خط و یا حجم است اما شدت نیرو به معنای میزان و اندازه نیرو میباشد. بنابراین میتوان اینگونه گفت که توزیع نیرو، تغییرات (آهنگ تغییرات) شدت (انداره) نیرو است.
در توزیع خطی، نیرو در طول یک خط وارد میشود و عرض محل اثر نیرو ناچیز است. مانند نیروی وارد بر یک کابل یا نیروی دیوار. واحد شدت نیرو در این حالت نیرو بر طول خط است و برحسب نیوتن بر متر (N/m) بیان میشود.
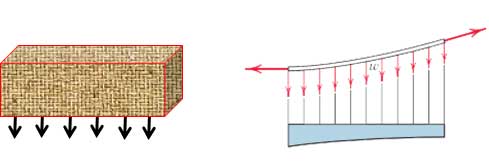
در توزیع سطحی، نیرو بر روی یک سطح مشخص توزیع شده است. مانند فشار آب پشت سد، نیروی باد و یا نیروی خاک مجاور دیوار زیرزمین. در سیالات این شدت نیرو را فشار (Pressure) و در جامدات به این شدت نیروی داخلی تنش (Stress) گفته میشود. واحد شدت نیرو در این حالت نیرو بر سطح است و برحسب نیوتن بر متر مربع (N/m2) بیان میشود.
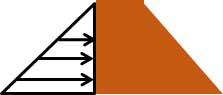
به عنوان یک نکته در یک مقطع عرضی از سد میتوان توزیع نیرو را بهصورت خطی در نظر گرفت.
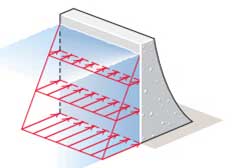
در توزیع حجمی، نیرو در حجم یک جسم توزیع میشود. مانند نیروی گرانش و نیروی تراوش در مکانیک خاک. واحد شدت نیرو در این حالت نیرو بر حجم است و برحسب نیوتن بر متر مکعب (N/m3) بیان میشود.
خوب است بدانیم که شدت نیروی گرانش را وزن مخصوص نیز مینامند. وزن مخصوص را با γ نمایش میدهند و برابر است با حاصل ضرب چگالی (ρ) در شتاب گرانش (g). بنابراین: (γ=ρg)
3- مرکز جرم
محل اثر برآیند نیروهای جاذبه (گرانش) را مرگز ثقل یا گرانیگاه جسم گوییم. برای یافتن مرکز ثقل میتوان از آزمایشی که شرح میشود استفاده نمود. جسمی با جرم m را از نقطه دلخواه A آویزان کرده. جسم در حال تعادل است و برآیند نیروها در امتداد طناب است. همین مراحل را با نقاط مانند B و C تکرار میکنیم.این خطوط اثر، همگی در یک نقطه موسوم به مرکز ثقل به هم میرسند.
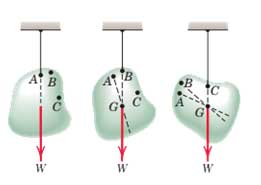
برای تعیین مکان مرکز ثقل یک جسم از اصل گشتاورها (تعمیم قضیه وارینون) استفاده میکنیم. بر این اساس گشتاور نیروی برآیند گرانش W حول هر محور دلخواهی برابر با مجموع گشتاورهای نیروهای گرانش dW وارد به هر یک از ذرات جسم حول آن محور است. بنابراین برآیند نیروی گرانش برابر با وزن جسم است.
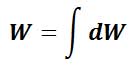
به عنوان مثال اصل گشتاورها حول محور y را مینویسیم:
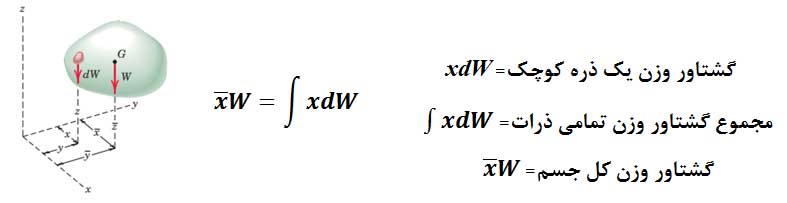
بنابراین روابط مختصات مرکز ثقل به صورت زیر خواهد بود.
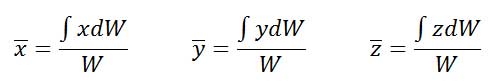
با جایگزینی W=mg و dW=gdm روابط بالا به صورت زیر خواهد بود. این روابط مستقل از اثرات گرانشی هستند و تنها تابعی از توزیع جرم است. بنابراین این روابط مختصات مرکز جرم را نشان میدهند
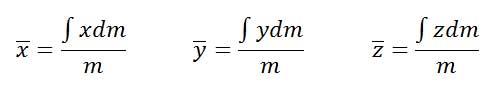
جرم یک جزء بسیار کوچک با حجم dV براساس رابطه چگالی برابر dm=ρdV خواهد بود. بنابراین جرم کل جسم به صورت زیر خواهد بود.
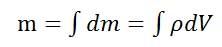
بنابراین روابط مختصات مرکز حجم بهصورت زیر میشود:
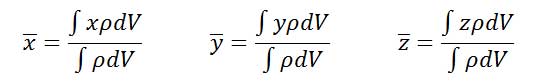
در محاسبات مرکز جرم، محورهای مختصات به نحوی انتخاب شود که با توجه به مرزهای فیزیکی جسم حل معادلات تا حد امکان ساده شود. هرگاه یک جسم همگن دارای خط یا صفحه تقارن باشد، یکی از محورهای مختصات را منطبق بر این خط یا صفحه انتخاب میکنیم. مرکز جرم همواره بر این خط یا صفحه تقارن واقع خواهد بود. زیرا گشتاور این ذرات نسبت به این خط یکدیگر را خنثی میکنند.
4- مرکز هندسی
اصطلاح مرکز هندسی را تنها زمانی بکار میبریم که محاسبات صرفا مربوط به یک شکل هندسی محض باشد. اگر چگالی در سراسر جسم یکنواخت باشد مرکز هندسی و مرکز جرم بر هم منطبق خواهند بود. بر اساس اینکه یک جسم واقعی را بهصورت یک خط (منحنی)، سطح و یا حجم بتوان مدلسازی کرد، مرکز هندسی اجسام محاسبه میشود.
برای محاسبه مرکز هندسی خط، یک میله نازک با طول L سطح مقطع A و چگالی ρ فرض میکنیم. اگر چگالی و سطح مقطع در طول خط (میله) ثابت باشد، مرکز هندسی بر مرکز جرم منطبق است. همچنین جرم یک جزء کوچک از آن خط برابر dm=ρAdL خواهد بود. با استفاده از روابط مرکز جرم داریم:
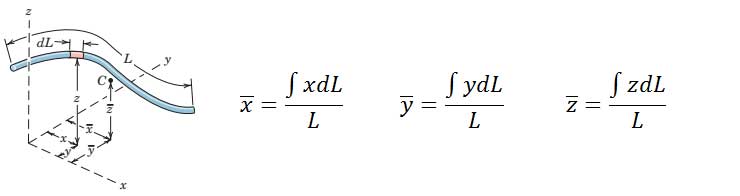
در حالت کلی مرکز هندسی یک خط میتواند بر آن واقع نباشد. اگر یک خط در صفحه x-y قرار گیرد برای یافتن مرکز هندسی آن تنها دو مولفه x̅ و ȳ نیاز است.
برای محاسبه مرکز سطح، یک پوسته جدار نازک با ضخامت کوچک اما ثابت t را فرض میکنیم.اگر ρ و t ثابت باشند، مرکز هندسی بر مرکز جرم منطبق است. همچنین مساحت سطح را برابر A میگیریم. بنابراین با استفاده از روابط مرکز جرم داریم:
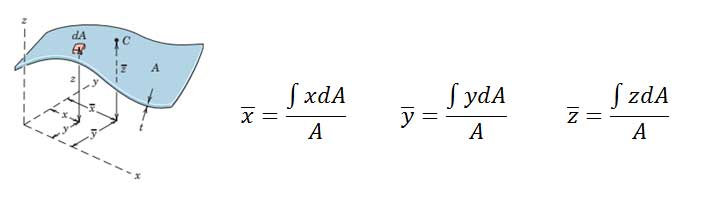
صورت کسرها در معادلات بالا را گشتاور اول سطح (First Moments of Area) مینامند.
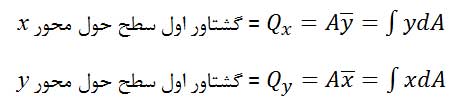
در حالت کلی مرکز هندسی سطوح منحنی بر آن واقع نیست. اگر یک سطح در صفحه x-y قرار گیرد برای یافتن مرکز سطح تنها دو مولفه x̅ و ȳ نیاز است.
برای محاسبه مرکز حجم، یک جسم با حجم V و چگالی ρ فرض میکنیم. اگر ρ در کل جسم ثابت باشد، مرکز هندسی بر مرکز جرم منطبق است. همچنین جرم یک جزء کوچک از آن خط برابر dm=ρdV خواهد بود. با استفاده از روابط مرکز جرم داریم:
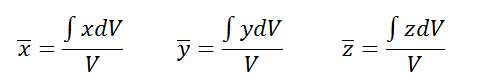
1-4- نکات انتخاب دیفرانسیل
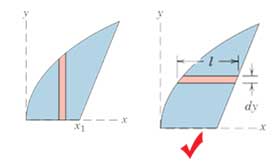
1- یک دیفرانسیل مرتبه اول را در مقایسه با دیفرانسیلهای مراتب بالاتر انتخاب کنید. در اینصورت تنها یکبار انتگرالگیری نیاز خواهیم داشت. به عنوان مثال در شکل زیر با انتخاب یک نوار افقی به عنوان دیفرانسیل سطح به صورت dA=ldy تنها به یک بار انتگرالگیری نسبت به y نیاز خواهیم داشت. در حالی که برای دیفرانسیل مرتبه دوم dxdy نیاز به دو بار انتگرالگیری، یک بار نسبت x به و بار دیگر نسبت به y نیاز خواهد بود.
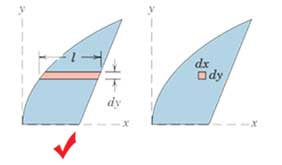
2- با یک بار انتگرال گیری پیوسته کل محدوده انتگرالگیری پوشش داده شود. برای مثال قطاع افقی در شکل زیر در مقایسه با قطاع عمودی ترجیح داده میشود. زیرا در صورت انتخاب قطاع عمودی به سبب ناپیوستگی تابع ارتفاع قطاع در x = x1 ناگزیر به دو بار انتگرالگیری در دو فاصله مجزا خواهیم بود.
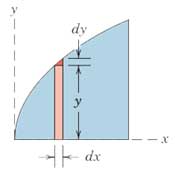
3- از جملات مرتبه بالا چشم پوشی شود. به عنوان مثال بهتر است که نوار عمودی سطح در زیر منحنی شکل زیر را با دیفرانسیل مرتبه اول dA=ydx بیان کنیم و از دیفرانسیل مرتبه دوم سطح مثلثی (dxdy)½ اجتناب نماییم.
4- محورهای مختصات بهگونهای انتخاب شود که بیشترین هماهنگی با مرزهای فیزیکی جسم مورد نظر داشته باشد.
5- برای بیان بازوی گشتاور دیفرانسیل برای محاسبه گشتاور آن، باید از مختصات مرکز هندسی دیفرانسیل استفاده کنیم. بنابراین روابط زیر برای بیان مختصات مرکز هندسی دیفرانسیل استفاده میشود.
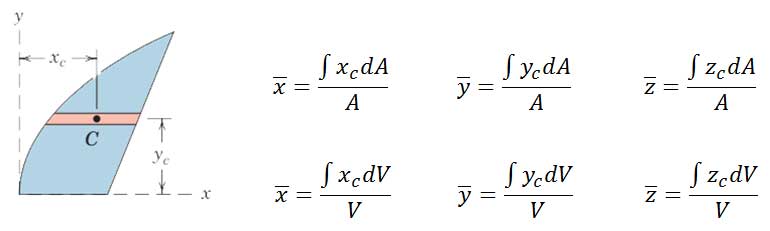
5- مسائل
برای فهم بهتر حل مسائل میتوانید به ویدیو مراجعه کنید.
1-5- مسئله 1
مرکز هندسی یک مثلث قائم زاویه را حساب کنید.
یک ضلع مثلث را بر محور x منطبق کردهایم.
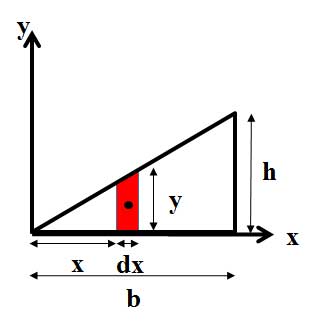
مساحت نوار باریک dA=ydx خواهد بود. حال با استفاده از تشابه مثلثها داریم:
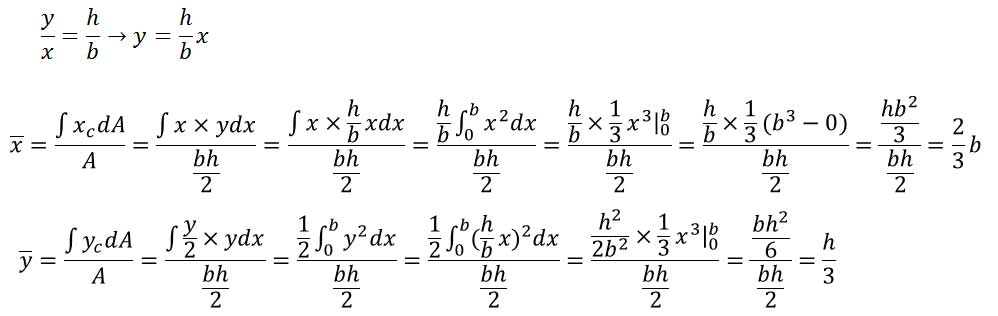
2-5- مسئله 2
مرکز هندسی شکل زیر را حساب کنید.
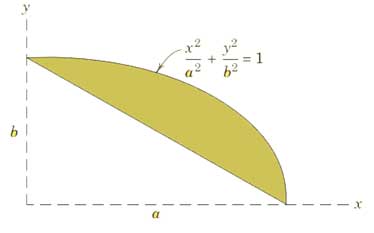
برای مشاهده حل این سوال به صفحه آموزش (حل تمرین استاتیک تمامی فصلها) مراجعه کنید.
6- روشهای تقریبی در تعیین مرکز هندسی اجسام مرکب
اگر بتوانیم یک جسم را به بخشهای متعدد تقسیم کنیم بهگونهای که مرکز جرم یا مرکز هندسی این بخشها به سادگی قابل محاسبه باشد، میتوان هر بخش را بهعنوان یک جزء محدود از کل در نظر گرفت و اصل گشتاورها را برای این مجموعه بکار گرفت. بنابراین در این حالت برای محاسبه مرکز جرم و مرکز سطح میتوان از روابط زیر استفاده کرد.

در این روش در صورت وجود حفره، جرم، سطح و یا حجم مورد نظر منفی در نظر گرفته میشود.
گشتاور اول سطح نیز در این حالت به صورت زیر قابل محاسبه است.
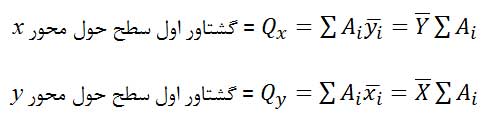
برای محاسبه مرکز سطح یک شکل هندسی نامنظم از روش تقریبی زیر استفاده میکنیم. برای مثال با توجه به به شکل زیر یک سطح نامنظم با مرکز هندسی C را در نظر بگیرید. مساحت المان قرمز رنگ با ارتفاع متغییر h به صورت A=hΔx خواهد بود. حال همانند روابط قبل در این حالت مختصات مرکز سطح به صورت زیر خواهد بود:

7- مسائل
برای فهم بهتر حل مسائل میتوانید به ویدیو مراجعه کنید.
1-7- مسئله 3
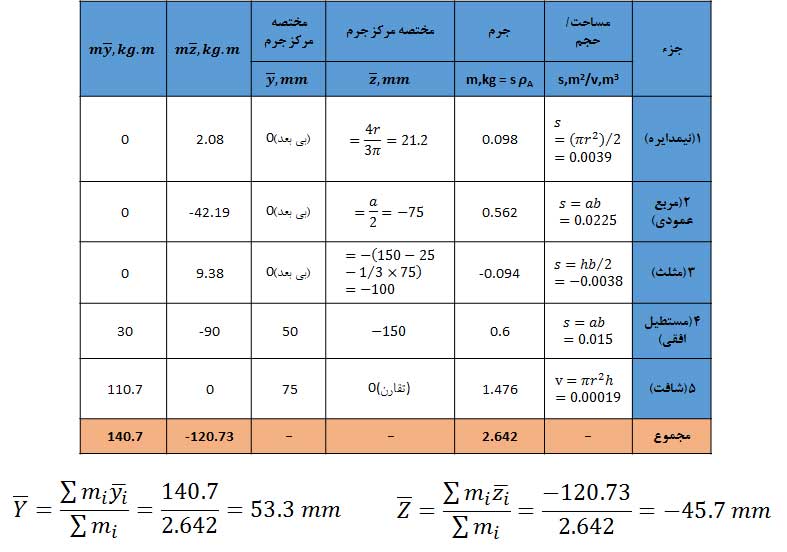
مرکز جرم جسم مرکب زیر را محاسبه کنید. سطح عمودی از ورقی با جرم واحد سطح 25kg/m2 است. جرم واحد سطح ورق افقی 40kg/m2 و چگالی شفت 7.83Mg/m3 است.
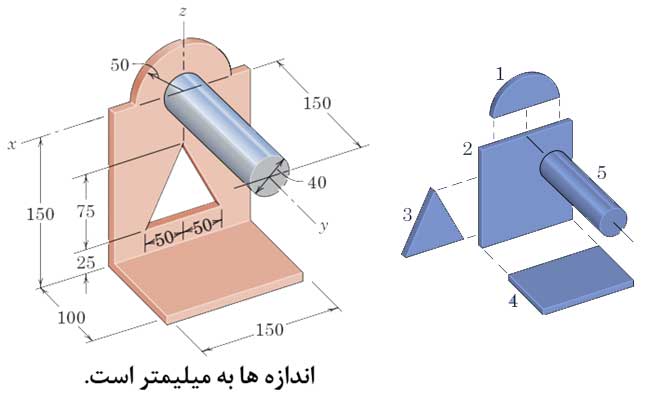
با توجه به اینکه جسم نسبت به محور z دارای تقارن است مختصه x̅ صفر است. اجزاء معادلات را در جدول زیر نوشتهایم.
2-7- مسئله 4
مرکز سطح تیر زیر را بیابید.
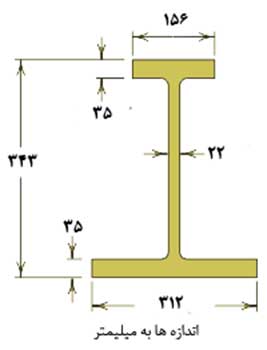
برای مشاهده حل این سوال به صفحه آموزش (حل تمرین استاتیک تمامی فصلها) مراجعه کنید.