تعادل بخش اول

1- آنچه در این آموزش خواهیم خواند…

فصل سوم کتاب استاتیک مریام در دو بخش آموزش داده شده است. این آموزش با عنوان تعادل در استاتیک مریام بخش 1 | دیاگرام آزاد و معادلات تعادل، بخش اول می‌باشد.

در این آموزش ابتدا شیوه رسم دیاگرام جسم آزاد را شرح خواهیم داد. در ادامه بحث نیر شرایط تعادل جسم را بررسی خواهیم کرد. در آموزش تعادل بخش دوم نیز به شرح مباحث قیدهای تکیه‌گاهی، معین و نامعین استاتیکی خواهیم پرداخت. در نهایت نیز نمونه مسائل حل خواهند شد.

2- رسم دیاگرام جسم آزاد

دیاگرام جسم آزاد، طرح ساده‌ای است از جسم یا مجموعه‌ای از اجسام منزوی شده، که در آن نیرو و یا نیروهایی که اجسام پیرامونی حذف شده بر جسم وارد می‌کنند نشان داده شده است. هدف از رسم دیاگرام جسم آزاد این است که جسم یا مجموعه‌ای از اجسام (سازه یا اجزا سازه‌ای) را از اجسام در تماس با آن‌ها جدا (منزوی) کنیم و نیروهایی که بر آن جسم یا مجموعه اجسام از طرف اجسام حذف شده وارد می‌شود را نشان دهیم.

قبل از رسم دیاگرام جسم آزاد باید ابتدا مشخصه‌های اصلی نیرو را بررسی نمود. در یک دسته‌بندی می‌توان نیروها را به دو دسته‌ی نیروهای تماسی و حجمی تقسیم نمود. نیروهای تماسی از تماس فیزیکی مستقیم دو جسم حاصل می‌شوند. مانند نیروهای وارد بر یک جسم از طرف سطح تکیه‌گاه. نیروهای حجمی از قرار گرفتن جسم در یک میدان نیرو حاصل می‌شوند. مانند وزن اجسام.

در دسته‌بندی دیگری می‌توان نیروها را به دو دسته نیروهای متمرکز و نیروهای گسترده تقسیم نمود. نیروهای متمرکز از عمل نیرو بر یک نقطه حاصل می‌شوند. اما نیروهای گسترده از عمل نیرو بر یک خط، سطح و یا یک حجم حاصل می‌شوند. در نوع دیگر دسته‌بندی نیروها به دو دسته نیروهای عمل (کنش) و نیروهای عکس‌العمل (واکنش) تقسیم می‌شوند. نیروهای عمل نیروهایی هستند که تمایل به حرکت جسم دارند و نیروهای عکس العمل نیروهایی هستند که باعث تعادل جسم می‌شوند.

1-2- تکیه‌گاه وعکس‌العمل‌های تکیه‌گاهی

محلی که جسم یا سازه به آن اتکا می‌کند و در آن نیروهای عکس العمل به سازه اعمال می‌شود را تکیه‌گاه گوییم. نیرویی که از تکیه گاه‌ها به جسم وارد می‌شود و تعادل جسم را حفظ می‌کند نیروی عکس‌العمل نامیده می‌شود.
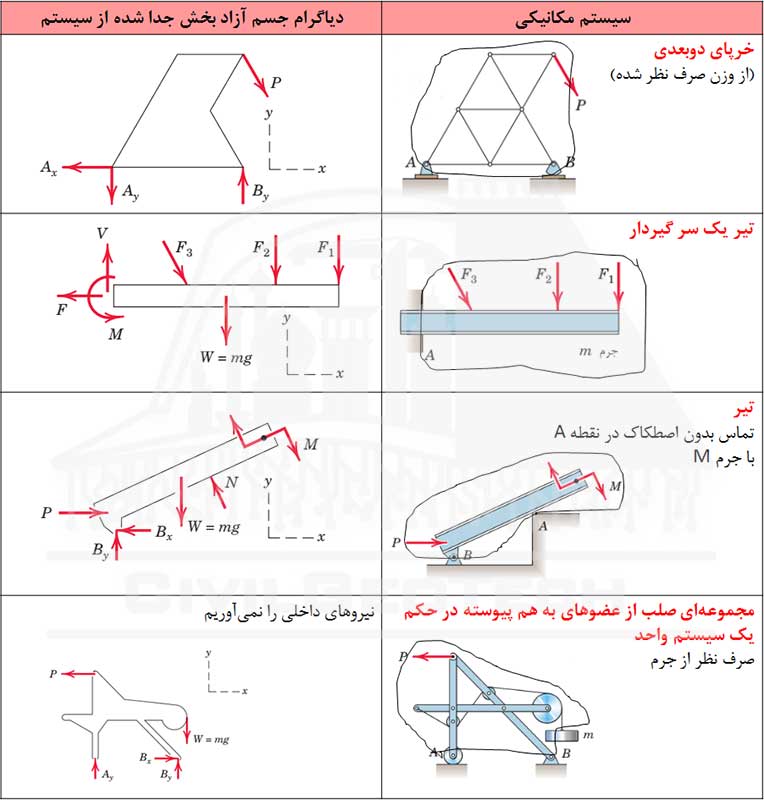
در شکل زیر شیوه‌های اعمال نیرو به سیستم‌های مکانیکی در تحلیل دو بعدی را نشان داده شده است. در هر مورد نیروی وارد از طرف اجسام پیرامونی به جسمی که قصد جداسازی آن را داریم نشان داده شده است. باید در نمایش نیروها به دقت قانون سوم نیوتن که بیان می‌کند یک نیروی عکس‌العمل هم‌اندازه و مخالف برای هر نیرو وجود دارد، رعایت شود.

در مورد ۱ ازجدول بالا به علت انعطاف پذیر بودن کابل‌ها، توانایی مقاومت در برابر نیروهای خمشی، برشی و یا فشاری را ندارند. از این رو تنها نیرویی که می توانند به جسم وارد کنند یک نیروی کششی است که در راستای مماس بر کابل در نقطه اتصال آن به جسم وارد می‌شود.

در مورد 2 ازجدول بالا، دو جسم با سطوح صیقلی در تماس با یکدیگر هستند. نیروی وارد از طرف یک جسم بر دیگری در امتداد عمود بر مماس مشترک سطوح تماس و به صورت فشاری است. در عمل هیچ سطحی کاملاً صیقلی نیست اما از این فرض می‌توان در حل بسیاری از مسائل استفاده کرد.

در مورد 3 ازجدول بالا، دو جسم با سطوح زبر در تماس با یکدیگر هستند. نیروی تماسی لزوماً در امتداد عمود بر مماس مشترک سطوح تماس نیست و می‌توان آن را به یک مؤلفه مماسی یا اصطکاکی F و یک مؤلفه عمودی N تجزیه کرد.

در مورد 4 ازجدول بالا، برخی از انواع تکیه‌گاه‌هایی که تا حد زیادی موجب حذف نیروهای اصطکاکی مماسی می‌شوند. را نشان میدهد. در اینگونه موارد، عکس العمل برآیند عمود بر سطح تکیه گاهی است.

در مورد 5 ازجدول بالا، به علت نبود اصطکاک، هیچ نیروی مقاومی به موازات میله یا شیار وجود ندارد.

در مورد 6 ازجدول بالا، این نوع اتصالات می‌توانند نیرو را در هر راستای عمود بر محور پین تحمل کنند. اثر نیروهای عکس‌العمل در پین‌ها را معمولاً به صورت دو مؤلفه متعامد نمایش می دهیم. جهت صحیح مؤلفه‌ها بستگی به نحوه بارگذاری بر روی عضو متصل به پین دارد. اگر نتوانیم جهت صحیح مؤلفه های عکس‌العمل را تعیین کنیم یک جهت را فرض می‌کنیم و بر مبنای جهت‌های فرضی معادلات تعادل را می‌نویسیم اگر پس از حل معادلات تعادل علامت مؤلفه مورد نظر مثبت باشد، یعنی جهت فرضی صحیح می باشد و اگر علامت آن منفی باشد، یعنی جهت انتخابی در خلاف جهت واقعی است.

در مورد 7 ازجدول بالا، جهت عکس العمل‌ها و کوپل خمشی در مسئله به نحوه بارگذاری بر روی عضو بستگی دارد.

در مورد 8 ازجدول بالا، اثر جاذبه گرانشی را به عنوان یکی از متداولترین نیروها نشان می‌دهد. برآیند نیروهای گرانشی وارد بر تمامی ذرات جسم برابر با وزن جسم W = mg است. این نیروی برآیند از مرکز جرم جسم G می‌گذرد و جهت آن برای اجسامی که در سطح زمین قرار دارند به سمت مرکز زمین است.

در مورد 9 ازجدول بالا، نیرویی که توسط یک فنر خطی در حالت کشش یا فشار وارد می‌شود از معادله F=kx بدست می‌آید. K سختی فنر و x تغییر طول آن نسبت به حالت آزاد است.

2-2- گام‌های رسم نمودار جسم آزاد

گام اول: انتخاب جسم یا مجموعه جسمی که قرار است منزوی شود (با توجه به مجهولات)

گام دوم: منزوی کردن جسم انتخابی (جداکردن آن و حذف سایر اجسام پیرامونی)(یک نقطه روی مرز خارجی انتخاب شده و با رسم خط ممتد به محل اول بر می‌گردیم)

گام سوم: اعمال نیروها بر جسم (نیروهایی که از طرف اجسام حذف شده بر جسم مورد نظر وارد می‌شوند)(نیروهای وارده را در نظر میگیریم نه واکنش ها)(از نیروهای قابل چشم پوشی مثل وزن صرف نظر کرد)(در صورتی که جهت یک نیرو مشخص نبود یک جهت را فرض می‌کنیم در صورت که پاسخ منفی شد جهت برعکس درست بوده است.)

گام چهارم: مشخص کردن دستگاه مختصات مناسب.
در جدول زیر نمونه‌ مثال‌هایی برای رسم دیاگرام آزاد جسم آورده شده است.

3- شرایط تعادل (Stability-Equilibrium)

1-3- معادلات تعادل

اگر یک جسم در حال تعادل باشد برآیند تمامی نیروها و گشتاورهای وارد بر آن صفر است. بنایراین معادلات تعادل به صورت زیر خواهد بود:
معادلات تعادل یک ذره در حالت دو بعد:

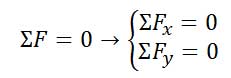
معادلات تعادل یک ذره در حالت سه بعد:

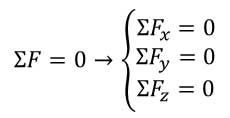
معادلات تعادل جسم در حالت دو بعد:

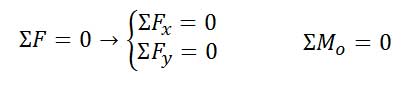
معادلات تعادل جسم در حالت سه بعد:

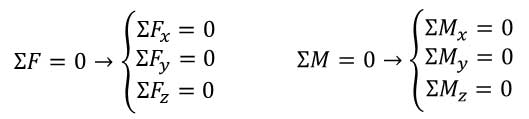
این شرایط لازم و کافی برای تعادل هستند. لازمند زیرا اگر برقرار نباشند توازن نیروها یا گشتاورها وجود نخواهد داشت. کافی هستند زیرا اگر برقرار باشند هیچ گونه عدم توازنی وجود نخواهد داشت.

2-3- حالات مختلف تعادل یک جسم

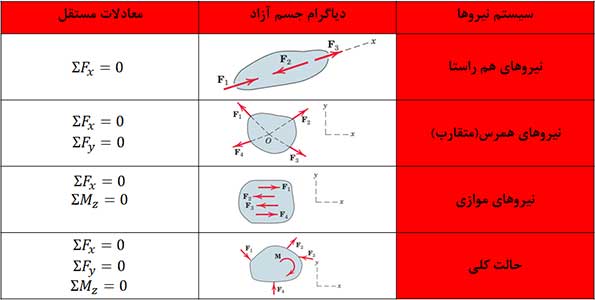
در جدول زیر ترکیب‌های مختلف سیستم‌های نیرو، وارد به اجسام دو بعدی در چهار نوع سیستم مختلف تقسیم بندی شده است.

1) تعادل نیروهای همراستا تنها نیازمند یک معادله تعادل در راستای این نیروها است. زیرا سایر معادلات خود به خود برقرارند.

2) تعادل نیروهای همرس در نقطه‌ای مانند O، تنها نیازمند دو معادله تعادل است. زیرا گشتاور این نیروها نسبت به نقطه O برابر صفر است. به بیان دیگر معادله سوم خود به خود برقرار است. از آنجا که نیروهای وارد به یک ذره لزوماً از یک نقطه می‌گذرند، تعادل ذرات در این گروه جای می‌گیرد.

3) تعادل نیروهای موازی هم صفحه نیازمند یک معادله تعادل در راستای این نیروها و یک معادله گشتاور حول یک محور عمود بر صفحه نیروها است.

4) تعادل یک سیستم کلی از نیروهای هم صفحه نیازمند دو معادله تعادل نیروها در صفحه x-y و یک معادله گشتاور حول یک محور عمود بر صفحه نیروها است.

در جدول زیر نیز شرایط تعادل برای عضوهای دو نیرویی و سه نیرویی بررسی شده است.

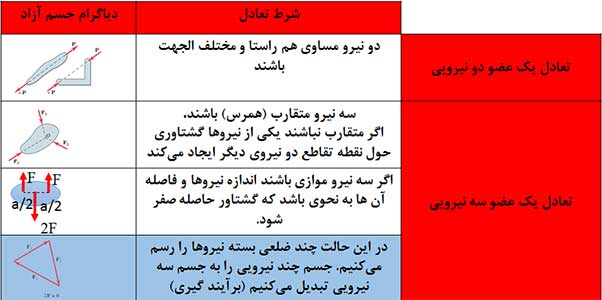
3-3- ترکیب‌های جایگزین برای حالت‌های مختلف معادلات تعادل

علاوه بر معادلات تعادل ذکر شده، دو روش دیگر برای بیان شرایط عمومی تعادل نیروها در دو بعد وجود دارد.
روش اول:
اگر ΣM_A=0 (زمانی رخ می‌دهد که برآیند نیروها یا باید صفر باشد یا از نقطه A عبور کند.) باشد، برآیند نیروها درصورت وجود نمی‌تواند کوپل باشد بلکه باید نیروی R باشد که از نقطه A می‌گذرد.

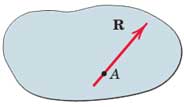
اگر ΣF_x=0 (زمانی رخ می‌دهد که مولفه بردار R در امتداد محور x صفر باشد. در واقع R یا صفر است یا بر x عمود می‌باشد.) باشد، نیروی برآیند R در صورت وجود علاوه بر اینکه باید از نقطه A بگذرد باید بر راستای x عمود باشد.

اگر ΣM_B=0 ( زمانی رخ می‌دهد که برآیند نیروها یا باید صفر باشد یا از نقطه B عبور کند.) باشد و B یک نقطه دلخواه باشد به گونه‌ای که پاره خط AB بر راستای x عمود نباشد.
بنابراین در این حالت ترکیب جایگزین برای معادلات تعادل به صورت زیر است.

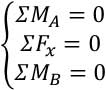
روش دوم:
با فرض اینکه A و B و C نقاط دلخواه باشند که روی یک راستا نباشند، داریم:
اگر ΣM_A=0 باشد، برآیند نیروها یا باید صفر باشد یا از نقطه A عبور کند.

اگر ΣM_B=0 باشد، برآیند نیروها یا باید صفر باشد یا از نقطه B عبور کند.

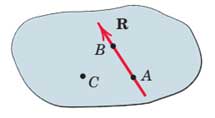
اگر ΣM_C=0 باشد، باید نیروی برآیند برابر صفر باشد زیرا دیگر نمی‌تواند از C بگذرد.
بنابراین در این حالت ترکیب جایگزین برای معادلات تعادل به صورت زیر است.

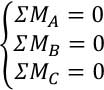
به عنوان یک نکته حتما باید ترکیب معادلات تعادل به گونه‌ای باشد که معادلات از یکدیگر مستقل باشند. زیرا در غیر اینصورت نتیجه بدیهی 0=0 حاصل می‌شود.

4- مراجع

Meriam, J. L.  and Kraige, L. G. (2011). Engineering Mechanics Volume 1: Statics. 7th ed. ‎John Wiley and Sons Inc